
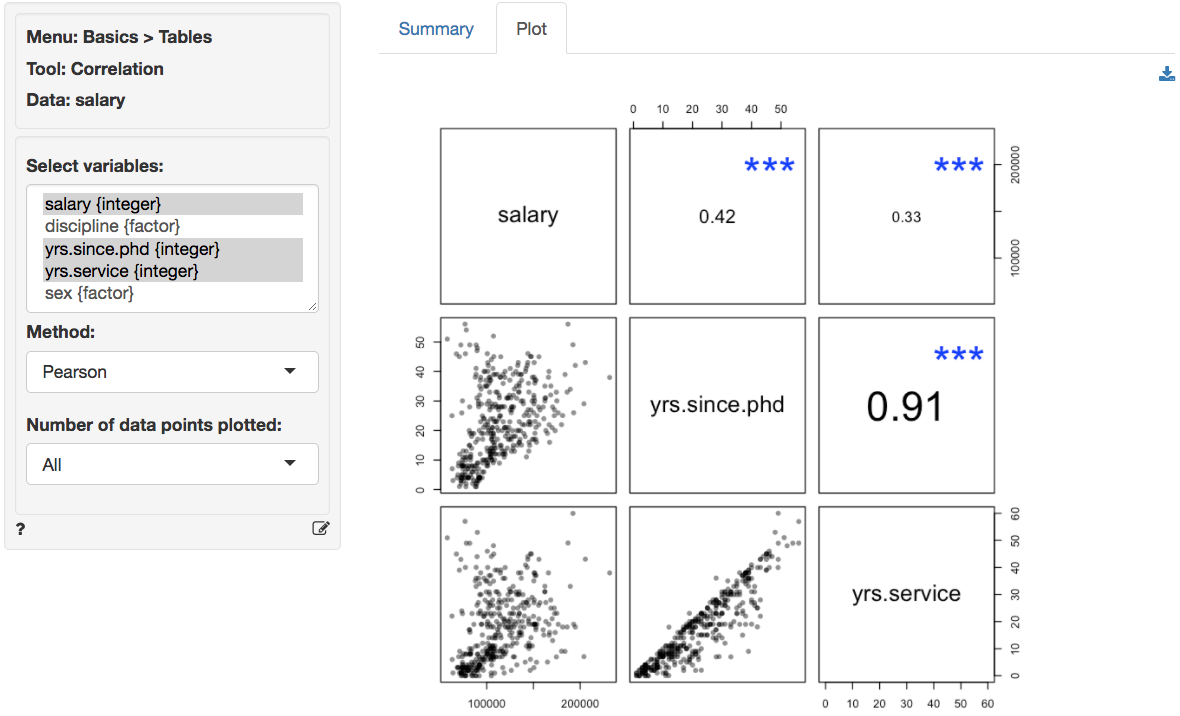
A time series is a sequence of floating-point decimal numbers (double values). Here is a formal definition of the autocorrelation function: Similarly, a value of -1 for a lag of k indicates a negative correlation with the values occuring k values before. A value of 1 for a lag of k indicates a positive correlation with values occuring k values before. The autocorrelation function can be viewed as a time series with values in the interval. To generate the correlation function of a time series, we will set a parameter called max_lag, and calculate all values of the autocorrelation function with a lag from 1 to max_lag.
Autocorrelation is defined based on the concept of lag. What is the autocorrelation function of a time series?Ĭalculating the autocorrelation function of a time series if useful to check if a time series is stationnary, or just generally to check if data points in a time series are correlated or not correlated with some previous data points occuring with a lag. The file "MainTestAutocorrelationFileToFile.java"in

If you want to execute this example from the command line,.

If you are using the graphical interface, (1)Ĭhoose the " Calculate_autocorrelation_of_time_series" algorithm, (2) select the input file " contextAutocorrelation.txt", (3) set the separator to the comma ',', set (4) maxlag = 15 and then (4) click " Run algorithm".This example explains how to calculate the autocorrelation function of time series using the SPMF open-source data mining library. And for the PACF, there is a sistem of equations that connect the ACF correlations to it, known as the Levinson recursion (which also is explained in that answer).Calculate the autocorrelation function of time series ( SPMF documentation) Then, you can get $\gamma_j$ and $\rho_j$ by the formula present in the most upvoted answer in ACF and PACF Formula. Obs: This is a more formal thing about statistics, ideally you should try to learn what exactly those things mean and how to see when you can make that assumption and when you can't, but it's best to ask that in another post. $$\bar + u_t$.įor using the data of your time series to calculate the amostral counterpart of those statistics (without having to set a model as what i presented untill now), first you need to assume that your series is at least weakly stationary and ergodic, which in loose terms is like saying that the series "will not change its statistical properties with time", so that the values of the series that you observe can be meaningful to the process behind it. Well if you mean how to estimate the ACF and PACF, here is how it's done:


 0 kommentar(er)
0 kommentar(er)
